Note
Go to the end to download the full example code
Scaling up Gaussian convolutions on 3D point clouds
Let’s compare the performance of PyTorch and KeOps on simple Gaussian RBF kernel products, as the number of samples grows from 100 to 1,000,000.
Note
In this demo, we use exact bruteforce computations (tensorized for PyTorch and online for KeOps), without leveraging any multiscale or low-rank (Nystroem/multipole) decomposition of the Kernel matrix. We are working on providing transparent support for these approximations in KeOps.
Setup
import numpy as np
import torch
from matplotlib import pyplot as plt
from benchmark_utils import flatten, random_normal, full_benchmark
use_cuda = torch.cuda.is_available()
print(
f"Running torch version {torch.__version__} with {'GPU' if use_cuda else 'CPU'}..."
)
Running torch version 2.6.0+cu124 with GPU...
Benchmark specifications:
# Numbers of samples that we'll loop upon:
problem_sizes = flatten(
[[1 * 10**k, 2 * 10**k, 5 * 10**k] for k in [2, 3, 4, 5]] + [[10**6]]
)
D = 3 # We work with 3D points
MAX_TIME = 0.1 # Run each experiment for at most 0.1 second
Synthetic dataset. Feel free to use a Stanford Bunny, or whatever!
def generate_samples(N, device="cuda", lang="torch", batchsize=1, **kwargs):
"""Generates two point clouds x, y and a scalar signal b of size N.
Args:
N (int): number of point.
device (str, optional): "cuda", "cpu", etc. Defaults to "cuda".
lang (str, optional): "torch", "numpy", etc. Defaults to "torch".
batchsize (int, optional): number of experiments to run in parallel. Defaults to None.
Returns:
3-uple of arrays: x, y, b
"""
randn = random_normal(device=device, lang=lang)
x = randn((batchsize, N, D))
y = randn((batchsize, N, D))
b = randn((batchsize, N, 1))
return x, y, b
Define a simple Gaussian RBF product, using a tensorized implementation. Note that expanding the squared norm \(\|x-y\|^2\) as a sum \(\|x\|^2 - 2 \langle x, y \rangle + \|y\|^2\) allows us to leverage the fast matrix-matrix product of the BLAS/cuBLAS libraries.
def gaussianconv_numpy(x, y, b, **kwargs):
"""(1,N,D), (1,N,D), (1,N,1) -> (1,N,1)"""
# N.B.: NumPy does not really support batch matrix multiplications:
x, y, b = x.squeeze(0), y.squeeze(0), b.squeeze(0)
D_xx = np.sum((x**2), axis=-1)[:, None] # (N,1)
D_xy = x @ y.T # (N,D) @ (D,M) = (N,M)
D_yy = np.sum((y**2), axis=-1)[None, :] # (1,M)
D_xy = D_xx - 2 * D_xy + D_yy # (N,M)
K_xy = np.exp(-D_xy) # (B,N,M)
return K_xy @ b
def gaussianconv_pytorch_eager(x, y, b, tf32=False, cdist=False, **kwargs):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
# If False, we stick to float32 computations.
# If True, we use TensorFloat32 whenever possible.
# As of PyTorch 2.0, this has no impact on run times so we
# do not use this option.
torch.backends.cuda.matmul.allow_tf32 = tf32
# We may use the cdist function to compute the squared norms:
if cdist:
D_xy = torch.cdist(x, y, p=2) # (B,N,M)
else:
D_xx = (x * x).sum(-1).unsqueeze(2) # (B,N,1)
D_xy = torch.matmul(x, y.permute(0, 2, 1)) # (B,N,D) @ (B,D,M) = (B,N,M)
D_yy = (y * y).sum(-1).unsqueeze(1) # (B,1,M)
D_xy = D_xx - 2 * D_xy + D_yy # (B,N,M)
K_xy = (-D_xy).exp() # (B,N,M)
return K_xy @ b # (B,N,1)
PyTorch 2.0 introduced a new compiler that improves speed and memory usage.
We use it with dynamic shapes to avoid re-compilation for every value of N.
Please note that torch.compile(...) is still experimental:
we will update this demo with new PyTorch releases.
# N.B. currently PyTorch dynamic is not supported with Python version >= 3.12
import sys
test_dynamic = torch.__version__ >= "2.0" and sys.version_info < (3, 12)
if test_dynamic:
# Inner function to be compiled:
def _gaussianconv_pytorch(x, y, b):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
# Note that cdist is not currently supported by torch.compile with dynamic=True.
D_xx = (x * x).sum(-1).unsqueeze(2) # (B,N,1)
D_xy = torch.matmul(x, y.permute(0, 2, 1)) # (B,N,D) @ (B,D,M) = (B,N,M)
D_yy = (y * y).sum(-1).unsqueeze(1) # (B,1,M)
D_xy = D_xx - 2 * D_xy + D_yy # (B,N,M)
K_xy = (-D_xy).exp() # (B,N,M)
return K_xy @ b # (B,N,1)
# Compile the function:
gaussianconv_pytorch_compiled = torch.compile(_gaussianconv_pytorch, dynamic=True)
# Wrap it to ignore optional keyword arguments:
def gaussianconv_pytorch_dynamic(x, y, b, **kwargs):
return gaussianconv_pytorch_compiled(x, y, b)
# And apply our function to compile the function once and for all:
# On the GPU, if it is available:
_ = gaussianconv_pytorch_compiled(*generate_samples(1000))
# And on the CPU, in any case:
# _ = gaussianconv_pytorch_compiled(*generate_samples(1000, device="cpu"))
Define a simple Gaussian RBF product, using an online implementation:
from pykeops.torch import generic_sum
fun_gaussianconv_keops = generic_sum(
"Exp(-SqDist(X,Y)) * B", # Formula
"A = Vi(1)", # Output
"X = Vi({})".format(D), # 1st argument
"Y = Vj({})".format(D), # 2nd argument
"B = Vj(1)", # 3rd argument
)
fun_gaussianconv_keops_no_fast_math = generic_sum(
"Exp(-SqDist(X,Y)) * B", # Formula
"A = Vi(1)", # Output
"X = Vi({})".format(D), # 1st argument
"Y = Vj({})".format(D), # 2nd argument
"B = Vj(1)", # 3rd argument
use_fast_math=False,
)
def gaussianconv_keops(x, y, b, backend="GPU", **kwargs):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
x, y, b = x.squeeze(), y.squeeze(), b.squeeze()
return fun_gaussianconv_keops(x, y, b, backend=backend)
def gaussianconv_keops_no_fast_math(x, y, b, backend="GPU", **kwargs):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
x, y, b = x.squeeze(), y.squeeze(), b.squeeze()
return fun_gaussianconv_keops_no_fast_math(x, y, b, backend=backend)
Finally, perform the same operation with our high-level pykeops.torch.LazyTensor wrapper:
from pykeops.torch import LazyTensor
def gaussianconv_lazytensor(x, y, b, backend="GPU", **kwargs):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
x_i = LazyTensor(x.unsqueeze(-2)) # (B, M, 1, D)
y_j = LazyTensor(y.unsqueeze(-3)) # (B, 1, N, D)
D_ij = ((x_i - y_j) ** 2).sum(-1) # (B, M, N, 1)
K_ij = (-D_ij).exp() # (B, M, N, 1)
S_ij = K_ij * b.unsqueeze(-3) # (B, M, N, 1) * (B, 1, N, 1)
return S_ij.sum(dim=2, backend=backend)
NumPy vs. PyTorch vs. KeOps (Gpu)
if use_cuda:
routines = [
(gaussianconv_numpy, "Numpy (CPU)", {"lang": "numpy"}),
(gaussianconv_pytorch_eager, "PyTorch (GPU, matmul)", {"cdist": False}),
(gaussianconv_pytorch_eager, "PyTorch (GPU, cdist)", {"cdist": True}),
]
if test_dynamic:
routines.append(
(
gaussianconv_pytorch_dynamic,
"PyTorch (GPU, compiled with dynamic shapes)",
{},
)
)
routines += [
(gaussianconv_lazytensor, "KeOps (GPU, LazyTensor)", {}),
(
gaussianconv_lazytensor,
"KeOps (GPU, LazyTensor, batchsize=100)",
{"batchsize": 100},
),
(gaussianconv_keops, "KeOps (GPU, Genred)", {}),
(gaussianconv_keops_no_fast_math, "KeOps (GPU, use_fast_math=False)", {}),
]
full_benchmark(
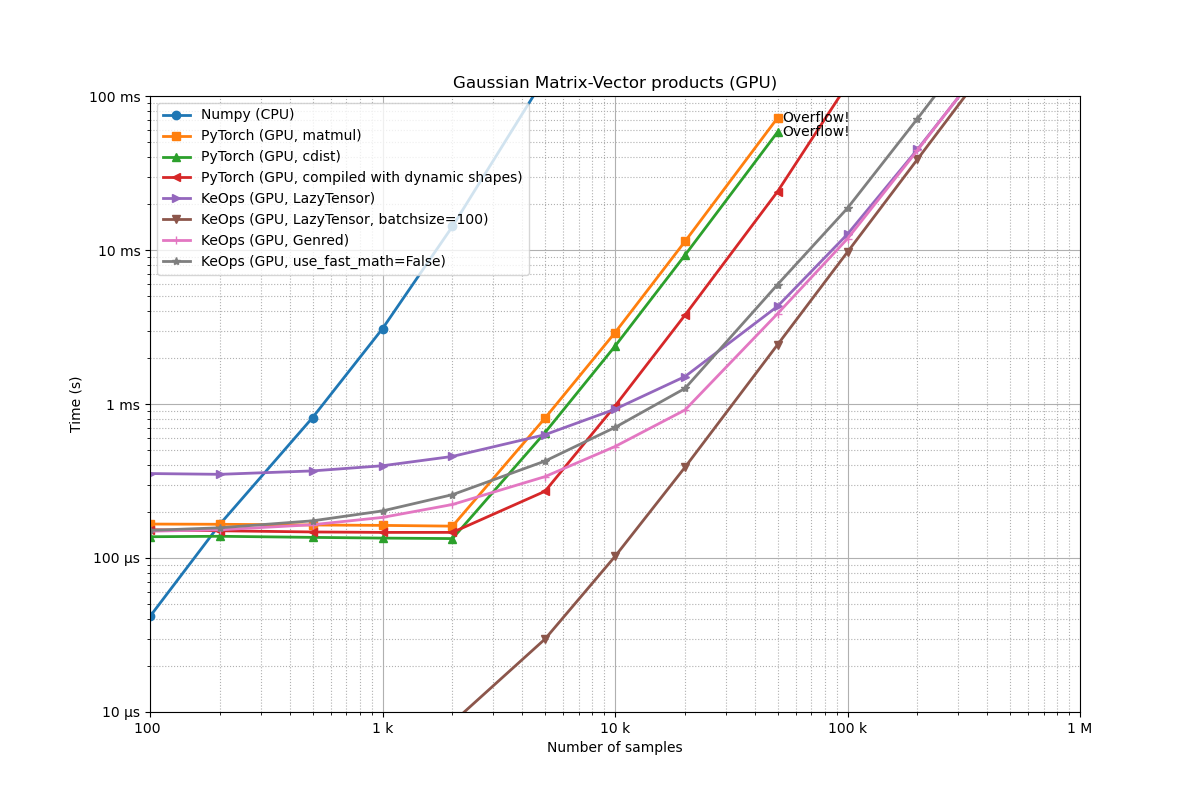
"Gaussian Matrix-Vector products (GPU)",
routines,
generate_samples,
problem_sizes=problem_sizes,
max_time=MAX_TIME,
)
Benchmarking : Gaussian Matrix-Vector products (GPU) ===============================
Numpy (CPU) -------------
1x100 loops of size 100 : 1x100x 33.7 µs
1x100 loops of size 200 : 1x100x 113.7 µs
1x100 loops of size 500 : 1x100x 687.7 µs
1x100 loops of size 1 k: 1x100x 2.4 ms
1x 10 loops of size 2 k: 1x 10x 11.1 ms
1x 1 loops of size 5 k: 1x 1x 131.5 ms
** Too slow!
PyTorch (GPU, matmul) -------------
1x100 loops of size 100 : 1x100x 118.1 µs
1x100 loops of size 200 : 1x100x 118.1 µs
1x100 loops of size 500 : 1x100x 118.3 µs
1x100 loops of size 1 k: 1x100x 118.0 µs
1x100 loops of size 2 k: 1x100x 255.0 µs
1x100 loops of size 5 k: 1x100x 1.4 ms
1x 10 loops of size 10 k: 1x 10x 5.7 ms
1x 10 loops of size 20 k: 1x 10x 22.6 ms
CUDA out of memory. Tried to allocate 9.31 GiB. GPU 0 has a total capacity of 23.68 GiB of which 3.35 GiB is free. Including non-PyTorch memory, this process has 20.30 GiB memory in use. Of the allocated memory 18.64 GiB is allocated by PyTorch, and 24.55 MiB is reserved by PyTorch but unallocated. If reserved but unallocated memory is large try setting PYTORCH_CUDA_ALLOC_CONF=expandable_segments:True to avoid fragmentation. See documentation for Memory Management (https://pytorch.org/docs/stable/notes/cuda.html#environment-variables)
** Runtime error!
PyTorch (GPU, cdist) -------------
1x100 loops of size 100 : 1x100x 261.7 µs
1x100 loops of size 200 : 1x100x 146.2 µs
1x100 loops of size 500 : 1x100x 126.3 µs
1x100 loops of size 1 k: 1x100x 125.9 µs
1x100 loops of size 2 k: 1x100x 222.0 µs
1x100 loops of size 5 k: 1x100x 1.2 ms
1x 10 loops of size 10 k: 1x 10x 4.7 ms
1x 10 loops of size 20 k: 1x 10x 18.9 ms
CUDA out of memory. Tried to allocate 9.31 GiB. GPU 0 has a total capacity of 23.68 GiB of which 3.35 GiB is free. Including non-PyTorch memory, this process has 20.30 GiB memory in use. Of the allocated memory 18.64 GiB is allocated by PyTorch, and 22.93 MiB is reserved by PyTorch but unallocated. If reserved but unallocated memory is large try setting PYTORCH_CUDA_ALLOC_CONF=expandable_segments:True to avoid fragmentation. See documentation for Memory Management (https://pytorch.org/docs/stable/notes/cuda.html#environment-variables)
** Runtime error!
KeOps (GPU, LazyTensor) -------------
1x100 loops of size 100 : 1x100x 411.5 µs
1x100 loops of size 200 : 1x100x 388.0 µs
1x100 loops of size 500 : 1x100x 390.1 µs
1x100 loops of size 1 k: 1x100x 548.8 µs
1x100 loops of size 2 k: 1x100x 420.3 µs
1x100 loops of size 5 k: 1x100x 482.3 µs
1x100 loops of size 10 k: 1x100x 584.1 µs
1x100 loops of size 20 k: 1x100x 879.4 µs
1x100 loops of size 50 k: 1x100x 2.9 ms
1x 10 loops of size 100 k: 1x 10x 9.4 ms
1x 10 loops of size 200 k: 1x 10x 34.9 ms
1x 1 loops of size 500 k: 1x 1x 212.4 ms
** Too slow!
KeOps (GPU, LazyTensor, batchsize=100) -------------
100x100 loops of size 100 : 100x100x 3.9 µs
100x100 loops of size 200 : 100x100x 4.0 µs
100x100 loops of size 500 : 100x100x 4.3 µs
100x100 loops of size 1 k: 100x100x 5.2 µs
100x100 loops of size 2 k: 100x100x 7.8 µs
100x100 loops of size 5 k: 100x100x 25.5 µs
100x100 loops of size 10 k: 100x100x 89.7 µs
100x100 loops of size 20 k: 100x100x 343.2 µs
100x100 loops of size 50 k: 100x100x 2.1 ms
100x 10 loops of size 100 k: 100x 10x 8.4 ms
100x 10 loops of size 200 k: 100x 10x 33.4 ms
100x 1 loops of size 500 k: 100x 1x 208.6 ms
** Too slow!
KeOps (GPU, Genred) -------------
1x100 loops of size 100 : 1x100x 129.2 µs
1x100 loops of size 200 : 1x100x 132.5 µs
1x100 loops of size 500 : 1x100x 138.8 µs
1x100 loops of size 1 k: 1x100x 149.0 µs
1x100 loops of size 2 k: 1x100x 170.7 µs
1x100 loops of size 5 k: 1x100x 235.2 µs
1x100 loops of size 10 k: 1x100x 327.7 µs
1x100 loops of size 20 k: 1x100x 633.6 µs
1x100 loops of size 50 k: 1x100x 2.7 ms
1x 10 loops of size 100 k: 1x 10x 9.2 ms
1x 10 loops of size 200 k: 1x 10x 34.8 ms
1x 1 loops of size 500 k: 1x 1x 210.5 ms
** Too slow!
KeOps (GPU, use_fast_math=False) -------------
1x100 loops of size 100 : 1x100x 131.8 µs
1x100 loops of size 200 : 1x100x 134.1 µs
1x100 loops of size 500 : 1x100x 144.9 µs
1x100 loops of size 1 k: 1x100x 160.6 µs
1x100 loops of size 2 k: 1x100x 189.6 µs
1x100 loops of size 5 k: 1x100x 273.4 µs
1x100 loops of size 10 k: 1x100x 412.6 µs
1x100 loops of size 20 k: 1x100x 890.1 µs
1x100 loops of size 50 k: 1x100x 4.1 ms
1x 10 loops of size 100 k: 1x 10x 14.1 ms
1x 1 loops of size 200 k: 1x 1x 52.5 ms
1x 1 loops of size 500 k: 1x 1x 321.7 ms
** Too slow!
We make several observations:
Asymptotically, all routines scale in O(N^2): multiplying N by 10 increases the computation time by a factor of 100. This is expected, since we are performing bruteforce computations. However, constants vary wildly between different implementations.
The NumPy implementation is slow, and prevents us from working efficiently with more than 10k points at a time.
The PyTorch GPU implementation is typically 100 times faster than the NumPy CPU code.
The
torch.compile(...)function, introduced by PyTorch 2.0, is making a real difference. It outperforms eager mode by a factor of 2 to 3.The CUDA kernel generated by KeOps is faster and more scalable than the PyTorch GPU implementation.
All GPU implementations have a constant overhead (< 1ms) which makes them less attractive when working with a single, small point cloud.
This overhead is especially large for the convenient
LazyTensorsyntax. As detailed below, this issue can be mitigated through the use of a batch dimension.
NumPy vs. PyTorch vs. KeOps (Cpu)
routines = [
(gaussianconv_numpy, "Numpy (CPU)", {"device": "cpu", "lang": "numpy"}),
(
gaussianconv_pytorch_eager,
"PyTorch (CPU, matmul)",
{"device": "cpu", "cdist": False},
),
(
gaussianconv_pytorch_eager,
"PyTorch (CPU, cdist)",
{"device": "cpu", "cdist": True},
),
(
gaussianconv_lazytensor,
"KeOps (CPU, LazyTensor)",
{"device": "cpu", "backend": "CPU"},
),
(gaussianconv_keops, "KeOps (CPU, Genred)", {"device": "cpu", "backend": "CPU"}),
]
full_benchmark(
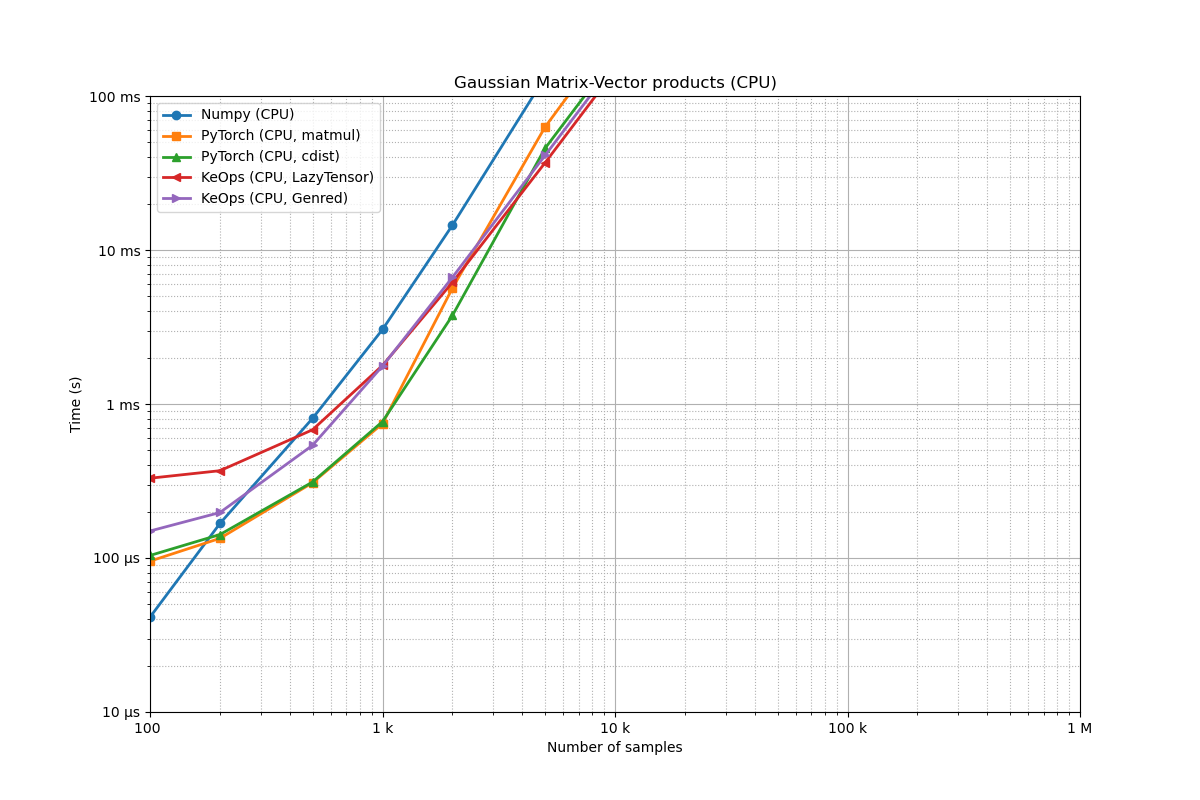
"Gaussian Matrix-Vector products (CPU)",
routines,
generate_samples,
problem_sizes=problem_sizes,
max_time=MAX_TIME,
)
Benchmarking : Gaussian Matrix-Vector products (CPU) ===============================
Numpy (CPU) -------------
1x100 loops of size 100 : 1x100x 33.5 µs
1x100 loops of size 200 : 1x100x 108.6 µs
1x100 loops of size 500 : 1x100x 663.5 µs
1x100 loops of size 1 k: 1x100x 2.2 ms
1x 10 loops of size 2 k: 1x 10x 11.1 ms
1x 1 loops of size 5 k: 1x 1x 126.8 ms
** Too slow!
PyTorch (CPU, matmul) -------------
1x100 loops of size 100 : 1x100x 86.2 µs
1x100 loops of size 200 : 1x100x 124.5 µs
1x100 loops of size 500 : 1x100x 176.8 µs
1x100 loops of size 1 k: 1x100x 315.5 µs
1x100 loops of size 2 k: 1x100x 3.5 ms
1x 10 loops of size 5 k: 1x 10x 54.9 ms
1x 1 loops of size 10 k: 1x 1x 198.4 ms
** Too slow!
PyTorch (CPU, cdist) -------------
1x100 loops of size 100 : 1x100x 87.5 µs
1x100 loops of size 200 : 1x100x 123.7 µs
1x100 loops of size 500 : 1x100x 177.8 µs
1x100 loops of size 1 k: 1x100x 299.6 µs
1x100 loops of size 2 k: 1x100x 2.1 ms
1x 10 loops of size 5 k: 1x 10x 34.6 ms
1x 1 loops of size 10 k: 1x 1x 127.3 ms
** Too slow!
KeOps (CPU, LazyTensor) -------------
1x100 loops of size 100 : 1x100x 320.7 µs
1x100 loops of size 200 : 1x100x 333.0 µs
1x100 loops of size 500 : 1x100x 559.2 µs
1x100 loops of size 1 k: 1x100x 1.2 ms
1x 10 loops of size 2 k: 1x 10x 3.8 ms
1x 10 loops of size 5 k: 1x 10x 21.7 ms
1x 1 loops of size 10 k: 1x 1x 86.0 ms
1x 1 loops of size 20 k: 1x 1x 342.1 ms
** Too slow!
KeOps (CPU, Genred) -------------
1x100 loops of size 100 : 1x100x 115.5 µs
1x100 loops of size 200 : 1x100x 165.9 µs
1x100 loops of size 500 : 1x100x 473.5 µs
1x100 loops of size 1 k: 1x100x 1.5 ms
1x 10 loops of size 2 k: 1x 10x 5.8 ms
1x 10 loops of size 5 k: 1x 10x 35.0 ms
1x 1 loops of size 10 k: 1x 1x 139.1 ms
** Too slow!
We note that the KeOps CPU implementation is typically slower than the PyTorch CPU implementation. This is because over the 2017-22 period, we prioritized “peak GPU performance” for research codes and provided a CPU backend mostly for testing and debugging. Going forward, as we work on making KeOps easier to integrate as a backend dependency in mature libraries, improving the performance of the KeOps CPU backend is a priority - both for compilation and runtime performance.
Genred vs. LazyTensor vs. batched LazyTensor
if use_cuda:
routines = [
(gaussianconv_keops, "KeOps (Genred)", {}),
(gaussianconv_lazytensor, "KeOps (LazyTensor)", {}),
(
gaussianconv_lazytensor,
"KeOps (LazyTensor, batchsize=10)",
{"batchsize": 10},
),
]
full_benchmark(
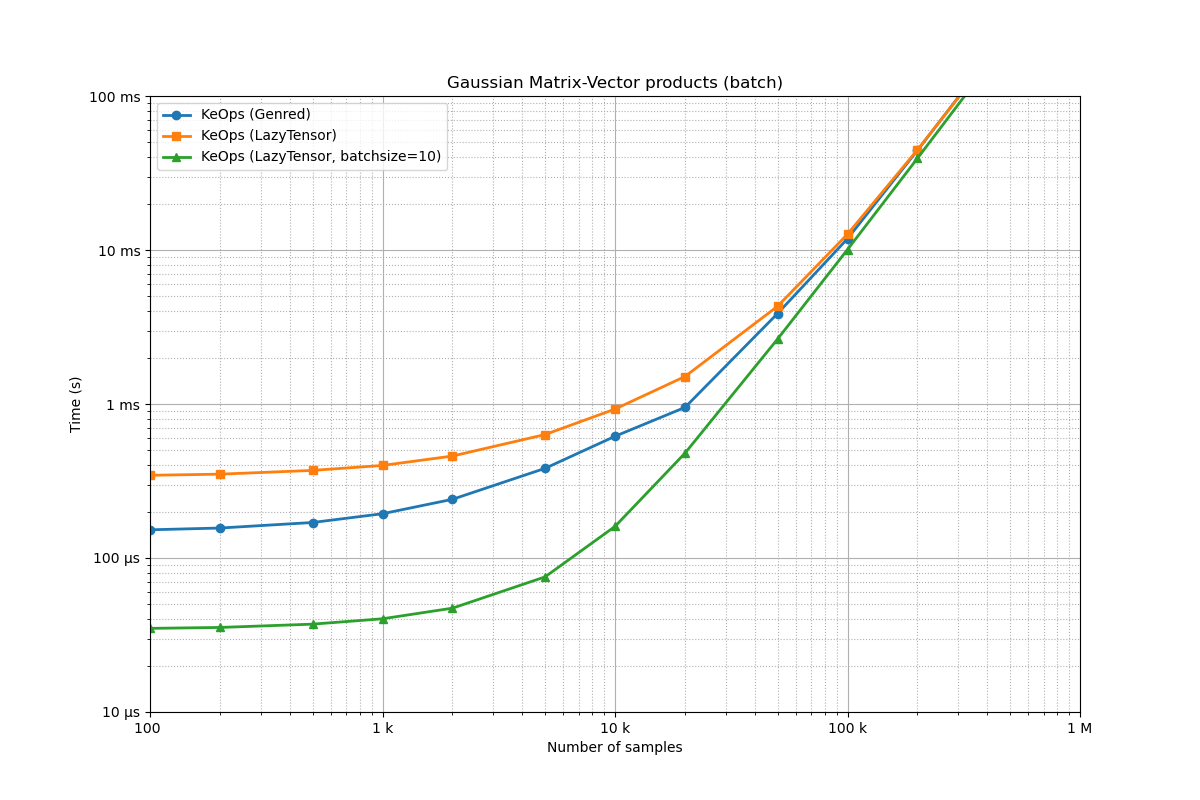
"Gaussian Matrix-Vector products (batch)",
routines,
generate_samples,
problem_sizes=problem_sizes,
max_time=MAX_TIME,
)
plt.show()
Benchmarking : Gaussian Matrix-Vector products (batch) ===============================
KeOps (Genred) -------------
1x100 loops of size 100 : 1x100x 130.1 µs
1x100 loops of size 200 : 1x100x 130.9 µs
1x100 loops of size 500 : 1x100x 139.4 µs
1x100 loops of size 1 k: 1x100x 153.2 µs
1x100 loops of size 2 k: 1x100x 175.1 µs
1x100 loops of size 5 k: 1x100x 240.0 µs
1x100 loops of size 10 k: 1x100x 349.7 µs
1x100 loops of size 20 k: 1x100x 679.8 µs
1x100 loops of size 50 k: 1x100x 2.7 ms
1x 10 loops of size 100 k: 1x 10x 9.1 ms
1x 10 loops of size 200 k: 1x 10x 34.5 ms
1x 1 loops of size 500 k: 1x 1x 210.4 ms
** Too slow!
KeOps (LazyTensor) -------------
1x100 loops of size 100 : 1x100x 383.5 µs
1x100 loops of size 200 : 1x100x 371.4 µs
1x100 loops of size 500 : 1x100x 378.7 µs
1x100 loops of size 1 k: 1x100x 369.8 µs
1x100 loops of size 2 k: 1x100x 416.9 µs
1x100 loops of size 5 k: 1x100x 487.1 µs
1x100 loops of size 10 k: 1x100x 589.2 µs
1x100 loops of size 20 k: 1x100x 881.8 µs
1x100 loops of size 50 k: 1x100x 2.9 ms
1x 10 loops of size 100 k: 1x 10x 9.5 ms
1x 10 loops of size 200 k: 1x 10x 34.9 ms
1x 1 loops of size 500 k: 1x 1x 211.9 ms
** Too slow!
KeOps (LazyTensor, batchsize=10) -------------
10x100 loops of size 100 : 10x100x 38.7 µs
10x100 loops of size 200 : 10x100x 34.4 µs
10x100 loops of size 500 : 10x100x 39.2 µs
10x100 loops of size 1 k: 10x100x 40.6 µs
10x100 loops of size 2 k: 10x100x 39.9 µs
10x100 loops of size 5 k: 10x100x 64.7 µs
10x100 loops of size 10 k: 10x100x 129.0 µs
10x100 loops of size 20 k: 10x100x 381.9 µs
10x100 loops of size 50 k: 10x100x 2.2 ms
10x 10 loops of size 100 k: 10x 10x 8.5 ms
10x 10 loops of size 200 k: 10x 10x 33.7 ms
10x 1 loops of size 500 k: 10x 1x 209.0 ms
** Too slow!
As expected, using a batch dimension reduces the relative overhead of
the LazyTensor syntax.
Total running time of the script: (2 minutes 21.030 seconds)