Radial kernels convolutions

This benchmark compares the performances of KeOps versus Numpy and PyTorch on various radial kernels convolutions. Namely it computes:

\[a_i = \sum_{j=1}^N f\Big(\frac{\|x_i-y_j\|}{\sigma}\Big) b_j, \quad \text{ for all } i=1,\cdots,M\]

where \(f\) is a Gauss or Cauchy or Laplace or inverse multiquadric kernel. See e.g. wikipedia

Setup

Standard imports:

import numpy as np
import timeit
import matplotlib
from matplotlib import pyplot as plt
from pykeops.numpy.utils import np_kernel
from pykeops.torch.utils import torch_kernel
from pykeops.torch import Vi, Vj, Pm

Benchmark specifications:

M = 10000  # Number of points x_i
N = 10000  # Number of points y_j
D = 3  # Dimension of the x_i's and y_j's
E = 3  # Dimension of the b_j's
REPEAT = 10  # Number of loops per test

dtype = "float32"

Create some random input data:

x = np.random.randn(M, D).astype(dtype)  # Target points
y = np.random.randn(N, D).astype(dtype)  # Source points
b = np.random.randn(N, E).astype(dtype)  # Source signal
sigma = np.array([2.4]).astype(dtype)  # Kernel radius

And load it as PyTorch variables:

try:
    import torch

    use_cuda = torch.cuda.is_available()
    device = "cuda" if use_cuda else "cpu"
    torchtype = torch.float32 if dtype == "float32" else torch.float64

    xc = torch.tensor(x, dtype=torchtype, device=device)
    yc = torch.tensor(y, dtype=torchtype, device=device)
    bc = torch.tensor(b, dtype=torchtype, device=device)
    sigmac = torch.tensor(sigma, dtype=torchtype, device=device)

except:
    pass

Convolution Benchmarks

We loop over four different kernels:

kernel_to_test = ["gaussian", "laplacian", "cauchy", "inverse_multiquadric"]
kernels = {
    "gaussian": lambda xc, yc, sigmac: (
        -Pm(1 / sigmac**2) * Vi(xc).sqdist(Vj(yc))
    ).exp(),
    "laplacian": lambda xc, yc, sigmac: (
        -(Pm(1 / sigmac**2) * Vi(xc).sqdist(Vj(yc))).sqrt()
    ).exp(),
    "cauchy": lambda xc, yc, sigmac: (
        1 + Pm(1 / sigmac**2) * Vi(xc).sqdist(Vj(yc))
    ).power(-1),
    "inverse_multiquadric": lambda xc, yc, sigmac: (
        1 + Pm(1 / sigmac**2) * Vi(xc).sqdist(Vj(yc))
    )
    .sqrt()
    .power(-1),
}

With four backends: Numpy, vanilla PyTorch, Generic KeOps reductions and a specific, handmade legacy CUDA code for kernel convolutions:

speed_numpy = {i: np.nan for i in kernel_to_test}
speed_pytorch = {i: np.nan for i in kernel_to_test}
speed_pykeops = {i: np.nan for i in kernel_to_test}


print("Timings for {}x{} convolutions:".format(M, N))

for k in kernel_to_test:
    print("kernel: " + k)

    # Pure numpy
    g_numpy = np.matmul(np_kernel(x, y, sigma, kernel=k), b)
    speed_numpy[k] = timeit.repeat(
        "gnumpy = np.matmul( np_kernel(x, y, sigma, kernel=k), b)",
        globals=globals(),
        repeat=5,
        number=1,
    )
    print("Time for NumPy:               {:.4f}s".format(np.median(speed_numpy[k])))

    # Vanilla pytorch (with cuda if available, and cpu otherwise)
    try:
        g_pytorch = torch_kernel(xc, yc, sigmac, kernel=k) @ bc
        torch.cuda.synchronize()
        speed_pytorch[k] = (
            np.array(
                timeit.repeat(
                    "torch_kernel(xc, yc, sigmac, kernel=k) @ bc; torch.cuda.synchronize()",
                    globals=globals(),
                    repeat=REPEAT,
                    number=4,
                )
            )
            / 4
        )

        print(
            "Time for PyTorch:             {:.4f}s".format(np.median(speed_pytorch[k])),
            end="",
        )
        print(
            "   (absolute error:       ",
            np.max(np.abs(g_pytorch.cpu().numpy() - g_numpy)),
            ")",
        )
    except:
        print("Time for PyTorch:             Not Done")

    # Keops: LazyTensors implementation (with cuda if available)
    try:
        g_pykeops = (kernels[k](xc, yc, sigmac) @ bc).cpu()
        torch.cuda.synchronize()
        speed_pykeops[k] = (
            np.array(
                timeit.repeat(
                    "kernels[k](xc, yc, sigmac) @ bc; torch.cuda.synchronize()",
                    globals=globals(),
                    repeat=REPEAT,
                    number=4,
                )
            )
            / 4
        )
        print(
            "Time for KeOps LazyTensors:       {:.4f}s".format(
                np.median(speed_pykeops[k])
            ),
            end="",
        )
        print(
            "   (absolute error:       ",
            np.max(np.abs(g_pykeops.data.numpy() - g_numpy)),
            ")",
        )
    except:
        print("Time for KeOps LazyTensors:       Not Done")

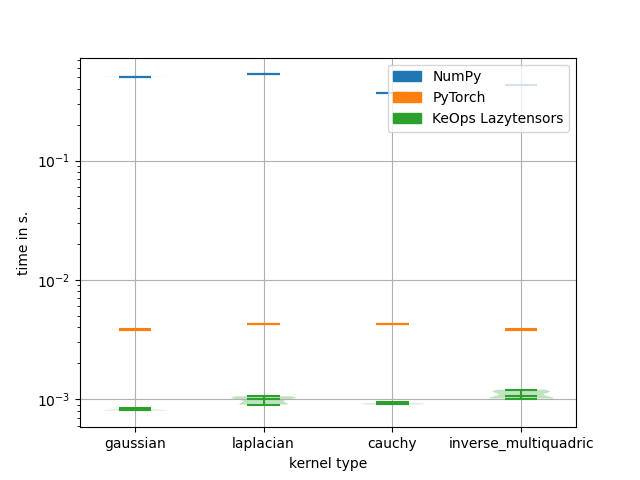
Timings for 10000x10000 convolutions:
kernel: gaussian
Time for NumPy:               0.5021s
Time for PyTorch:             0.0038s   (absolute error:        0.0008239746 )
Time for KeOps LazyTensors:       0.0008s   (absolute error:        0.00077819824 )
kernel: laplacian
Time for NumPy:               0.5265s
Time for PyTorch:             0.0043s   (absolute error:        0.0006637573 )
Time for KeOps LazyTensors:       0.0010s   (absolute error:        0.00064849854 )
kernel: cauchy
Time for NumPy:               0.3654s
Time for PyTorch:             0.0043s   (absolute error:        0.00091552734 )
Time for KeOps LazyTensors:       0.0009s   (absolute error:        0.0008621216 )
kernel: inverse_multiquadric
Time for NumPy:               0.4292s
Time for PyTorch:             0.0038s   (absolute error:        0.0010681152 )
Time for KeOps LazyTensors:       0.0011s   (absolute error:        0.0010070801 )

Display results

# plot violin plot
plt.violinplot(
    list(speed_numpy.values()),
    showmeans=False,
    showmedians=True,
)
plt.violinplot(
    list(speed_pytorch.values()),
    showmeans=False,
    showmedians=True,
)
plt.violinplot(
    list(speed_pykeops.values()),
    showmeans=False,
    showmedians=True,
)

plt.xticks([1, 2, 3, 4], kernel_to_test)
plt.yscale("log")
# plt.ylim((0, .01))

plt.grid(True)
plt.xlabel("kernel type")
plt.ylabel("time in s.")

cmap = plt.get_cmap("tab10")
fake_handles = [matplotlib.patches.Patch(color=cmap(i)) for i in range(4)]

plt.legend(
    fake_handles,
    ["NumPy", "PyTorch", "KeOps Lazytensors"],
    loc="best",
)

plt.show()