Note
Go to the end to download the full example code
Benchmarking Gaussian convolutions in high dimensions
Let’s compare the performances of PyTorch and KeOps on simple Gaussian RBF kernel products, as the dimension grows.
Setup
import torch
from matplotlib import pyplot as plt
from benchmark_utils import random_normal, full_benchmark
use_cuda = torch.cuda.is_available()
Benchmark specifications:
N = 10000 # Number of samples
# Dimensions to test:
Dims = [1, 3, 5, 10, 20, 30, 50, 80, 100, 120, 150, 200, 300, 500, 1000, 2000, 3000]
Synthetic dataset.
def generate_samples(D, device="cuda", lang="torch", batchsize=1, **kwargs):
"""Generates two point clouds x, y and a scalar signal b of size N.
Args:
D (int): dimension of the ambient space.
device (str, optional): "cuda", "cpu", etc. Defaults to "cuda".
lang (str, optional): "torch", "numpy", etc. Defaults to "torch".
batchsize (int, optional): number of experiments to run in parallel. Defaults to None.
Returns:
3-uple of arrays: x, y, b
"""
randn = random_normal(device=device, lang=lang)
x = randn((batchsize, N, D))
y = randn((batchsize, N, D))
b = randn((batchsize, N, 1))
return x, y, b
Define a simple Gaussian RBF product, using a tensorized implementation.
Note that expanding the squared norm
def gaussianconv_pytorch(x, y, b, tf32=False, **kwargs):
"""(B,N,D), (B,N,D), (B,N,1) -> (B,N,1)"""
# If False, we stick to float32 computations.
# If True, we use TensorFloat32 whenever possible.
torch.backends.cuda.matmul.allow_tf32 = tf32
D_xx = (x * x).sum(-1).unsqueeze(2) # (B,N,1)
D_xy = torch.matmul(x, y.permute(0, 2, 1)) # (B,N,D) @ (B,D,M) = (B,N,M)
D_yy = (y * y).sum(-1).unsqueeze(1) # (B,1,M)
D_xy = D_xx - 2 * D_xy + D_yy # (B,N,M)
K_xy = (-D_xy).exp() # (B,N,M)
return K_xy @ b # (B,N,1)
Define a simple Gaussian RBF product, using an online implementation:
from pykeops.torch import generic_sum
def gaussianconv_keops(x, y, b, backend="GPU", **kwargs):
D = x.shape[-1]
fun = generic_sum(
"Exp(X|Y) * B", # Formula
"A = Vi(1)", # Output
"X = Vi({})".format(D), # 1st argument
"Y = Vj({})".format(D), # 2nd argument
"B = Vj(1)", # 3rd argument
)
ex = (-(x * x).sum(-1)).exp()[:, :, None]
ey = (-(y * y).sum(-1)).exp()[:, :, None]
return ex * fun(2 * x, y, b * ey, backend=backend)
Same, but without the chunked computation mode:
def gaussianconv_keops_nochunks(x, y, b, backend="GPU", **kwargs):
D = x.shape[-1]
fun = generic_sum(
"Exp(X|Y) * B", # Formula
"A = Vi(1)", # Output
"X = Vi({})".format(D), # 1st argument
"Y = Vj({})".format(D), # 2nd argument
"B = Vj(1)", # 3rd argument
enable_chunks=False,
)
ex = (-(x * x).sum(-1)).exp()[:, :, None]
ey = (-(y * y).sum(-1)).exp()[:, :, None]
return ex * fun(2 * x, y, b * ey, backend=backend)
PyTorch vs. KeOps (Gpu)
routines = [
(gaussianconv_pytorch, "PyTorch (GPU, TF32=False)", {"tf32": False}),
(gaussianconv_pytorch, "PyTorch (GPU, TF32=True)", {"tf32": True}),
(gaussianconv_keops_nochunks, "KeOps < 1.4.2 (GPU)", {}),
(gaussianconv_keops, "KeOps >= 1.4.2 (GPU)", {}),
]
full_benchmark(
f"Gaussian Matrix-Vector products in high dimension, with N={N:,} (GPU)",
routines,
generate_samples,
problem_sizes=Dims,
xlabel="Dimension of the points",
)
plt.show()
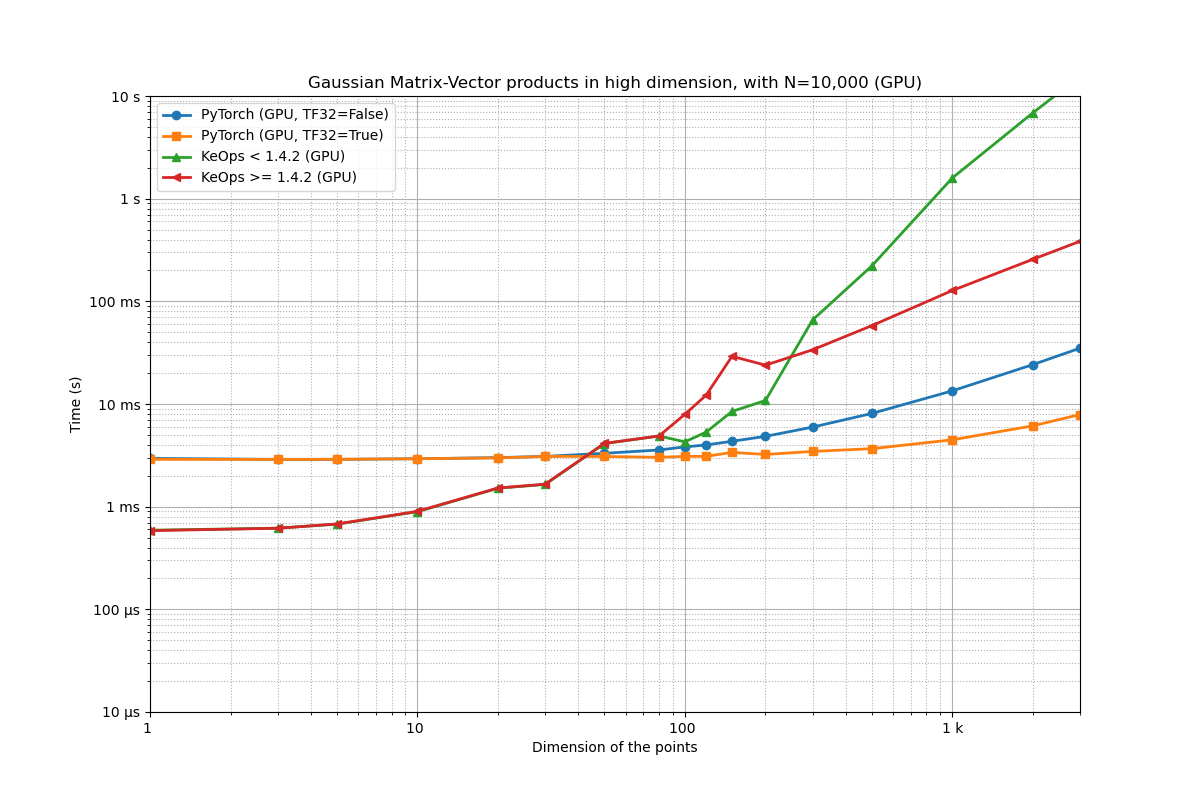
Benchmarking : Gaussian Matrix-Vector products in high dimension, with N=10,000 (GPU) ===============================
PyTorch (GPU, TF32=False) -------------
1x100 loops of size 1 : 1x100x 5.7 ms
1x100 loops of size 3 : 1x100x 5.7 ms
1x100 loops of size 5 : 1x100x 5.7 ms
1x100 loops of size 10 : 1x100x 5.7 ms
1x100 loops of size 20 : 1x100x 5.7 ms
1x100 loops of size 30 : 1x100x 5.9 ms
1x100 loops of size 50 : 1x100x 5.9 ms
1x100 loops of size 80 : 1x100x 6.1 ms
1x100 loops of size 100 : 1x100x 6.4 ms
1x100 loops of size 120 : 1x100x 6.5 ms
1x100 loops of size 150 : 1x100x 6.9 ms
1x100 loops of size 200 : 1x100x 7.3 ms
1x100 loops of size 300 : 1x100x 8.4 ms
1x100 loops of size 500 : 1x100x 10.5 ms
1x100 loops of size 1 k: 1x100x 15.9 ms
1x100 loops of size 2 k: 1x100x 27.2 ms
1x 10 loops of size 3 k: 1x 10x 38.5 ms
PyTorch (GPU, TF32=True) -------------
1x100 loops of size 1 : 1x100x 5.7 ms
1x100 loops of size 3 : 1x100x 5.7 ms
1x100 loops of size 5 : 1x100x 5.7 ms
1x100 loops of size 10 : 1x100x 5.7 ms
1x100 loops of size 20 : 1x100x 5.7 ms
1x100 loops of size 30 : 1x100x 5.8 ms
1x100 loops of size 50 : 1x100x 6.0 ms
1x100 loops of size 80 : 1x100x 6.0 ms
1x100 loops of size 100 : 1x100x 6.2 ms
1x100 loops of size 120 : 1x100x 6.3 ms
1x100 loops of size 150 : 1x100x 6.8 ms
1x100 loops of size 200 : 1x100x 6.7 ms
1x100 loops of size 300 : 1x100x 7.5 ms
1x100 loops of size 500 : 1x100x 8.6 ms
1x100 loops of size 1 k: 1x100x 11.5 ms
1x100 loops of size 2 k: 1x100x 17.3 ms
1x100 loops of size 3 k: 1x100x 23.3 ms
KeOps < 1.4.2 (GPU) -------------
1x100 loops of size 1 : 1x100x 510.8 µs
1x100 loops of size 3 : 1x100x 544.7 µs
1x100 loops of size 5 : 1x100x 587.7 µs
1x100 loops of size 10 : 1x100x 781.4 µs
1x100 loops of size 20 : 1x100x 1.1 ms
1x100 loops of size 30 : 1x100x 1.5 ms
1x100 loops of size 50 : 1x100x 4.1 ms
1x100 loops of size 80 : 1x100x 5.5 ms
1x100 loops of size 100 : 1x100x 8.7 ms
1x100 loops of size 120 : 1x100x 11.6 ms
1x100 loops of size 150 : 1x100x 11.0 ms
1x100 loops of size 200 : 1x100x 10.4 ms
1x100 loops of size 300 : 1x100x 98.2 ms
1x 10 loops of size 500 : 1x 10x 977.2 ms
1x 1 loops of size 1 k: 1x 1x 2.4 s
1x 1 loops of size 2 k: 1x 1x 9.5 s
1x 1 loops of size 3 k: 1x 1x 21.7 s
** Too slow!
KeOps >= 1.4.2 (GPU) -------------
1x100 loops of size 1 : 1x100x 509.2 µs
1x100 loops of size 3 : 1x100x 544.1 µs
1x100 loops of size 5 : 1x100x 582.6 µs
1x100 loops of size 10 : 1x100x 777.6 µs
1x100 loops of size 20 : 1x100x 1.1 ms
1x100 loops of size 30 : 1x100x 1.5 ms
1x100 loops of size 50 : 1x100x 4.0 ms
1x100 loops of size 80 : 1x100x 5.4 ms
1x100 loops of size 100 : 1x100x 9.5 ms
1x100 loops of size 120 : 1x100x 13.3 ms
1x100 loops of size 150 : 1x100x 27.0 ms
1x 10 loops of size 200 : 1x 10x 24.1 ms
1x 10 loops of size 300 : 1x 10x 35.1 ms
1x 10 loops of size 500 : 1x 10x 57.6 ms
1x 10 loops of size 1 k: 1x 10x 116.7 ms
1x 10 loops of size 2 k: 1x 10x 239.8 ms
1x 1 loops of size 3 k: 1x 1x 351.3 ms
Total running time of the script: (2 minutes 14.658 seconds)