Block-sparse reductions

This script showcases the use of the optional ranges argument to compute block-sparse reductions with sub-quadratic time complexity.

Setup

Standard imports:

import time

import numpy as np
from matplotlib import pyplot as plt

from pykeops.numpy import LazyTensor
import pykeops.config

dtype = "float32"

Define our dataset: two point clouds on the unit square.

M, N = (5000, 5000) if pykeops.config.gpu_available else (2000, 2000)

t = np.linspace(0, 2 * np.pi, M + 1)[:-1]
x = np.stack((0.4 + 0.4 * (t / 7) * np.cos(t), 0.5 + 0.3 * np.sin(t)), 1)
x = x + 0.01 * np.random.randn(*x.shape)
x = x.astype(dtype)

y = np.random.randn(N, 2).astype(dtype)
y = y / 10 + np.array([0.6, 0.6]).astype(dtype)

Computing a block-sparse reduction

On the GPU, contiguous memory accesses are key to high performances. To enable the implementation of algorithms with sub-quadratic time complexity under this constraint, KeOps provides access to block-sparse reduction routines through the optional ranges argument, which is supported by numpy.Genred and all its children.

Pre-processing

To leverage this feature through the pykeops.torch API, the first step is to clusterize your data into groups which should neither be too small (performances on clusters with less than ~200 points each are suboptimal) nor too many (the from_matrix() pre-processor can become a bottleneck when working with >2,000 clusters per point cloud).

In this tutorial, we use the grid_cluster() routine which simply groups points into cubic bins of arbitrary size:

from pykeops.numpy.cluster import grid_cluster

eps = 0.05  # Size of our square bins

Start = time.time()
start = time.time()
x_labels = grid_cluster(x, eps)  # class labels
y_labels = grid_cluster(y, eps)  # class labels
end = time.time()
print("Perform clustering       : {:.4f}s".format(end - start))

Perform clustering       : 0.0005s

Once (integer) cluster labels have been computed, we can compute the centroids and memory footprint of each class:

from pykeops.numpy.cluster import cluster_ranges_centroids

# Compute one range and centroid per class:
start = time.time()
x_ranges, x_centroids, _ = cluster_ranges_centroids(x, x_labels)
y_ranges, y_centroids, _ = cluster_ranges_centroids(y, y_labels)
end = time.time()
print("Compute ranges+centroids : {:.4f}s".format(end - start))

Compute ranges+centroids : 0.0002s

Finally, we can sort our points according to their labels, making sure that all clusters are stored contiguously in memory:

from pykeops.numpy.cluster import sort_clusters

start = time.time()
x, x_labels = sort_clusters(x, x_labels)
y, y_labels = sort_clusters(y, y_labels)
end = time.time()
print("Sort the points          : {:.4f}s".format(end - start))

Sort the points          : 0.0004s

Cluster-Cluster binary mask

The key idea behind KeOps’s block-sparsity mode is that as soon as data points are sorted, we can manage the reduction scheme through a small, coarse boolean mask whose values encode whether or not we should perform computations at a finer scale.

In this example, we compute a simple Gaussian convolution of radius \(\sigma\) and decide to skip points-to-points interactions between blocks whose centroids are further apart than \(4\sigma\), as \(\exp(- (4\sigma)^2 / 2\sigma^2 ) = e^{-8} \ll 1\), with 99% of the mass of a Gaussian kernel located in the \(3\sigma\) range.

sigma = 0.05  # Characteristic length of interaction
start = time.time()

# Compute a coarse Boolean mask:
D = np.sum((x_centroids[:, None, :] - y_centroids[None, :, :]) ** 2, 2)
keep = D < (4 * sigma) ** 2

To turn this mask into a set of integer Tensors which is more palatable to KeOps’s low-level CUDA API, we then use the from_matrix routine…

from pykeops.numpy.cluster import from_matrix

ranges_ij = from_matrix(x_ranges, y_ranges, keep)

end = time.time()
print("Process the ranges       : {:.4f}s".format(end - start))

End = time.time()
t_cluster = End - Start
print("Total time (synchronized): {:.4f}s".format(End - Start))
print("")

Process the ranges       : 0.0007s
Total time (synchronized): 0.0028s

And we’re done: here is the ranges argument that can be fed to the KeOps reduction routines! For large point clouds, we can expect a speed-up that is directly proportional to the ratio of mass between our fine binary mask (encoded in ranges_ij) and the full, N-by-M kernel matrix:

areas = (x_ranges[:, 1] - x_ranges[:, 0])[:, None] * (y_ranges[:, 1] - y_ranges[:, 0])[
    None, :
]
total_area = np.sum(areas)  # should be equal to N*M
sparse_area = np.sum(areas[keep])
print(
    "We keep {:.2e}/{:.2e} = {:2d}% of the original kernel matrix.".format(
        sparse_area, total_area, int(100 * sparse_area / total_area)
    )
)
print("")

We keep 3.39e+06/2.50e+07 = 13% of the original kernel matrix.

Benchmark a block-sparse Gaussian convolution

Define a Gaussian kernel matrix from 2d point clouds:

x_, y_ = x / sigma, y / sigma
x_i, y_j = LazyTensor(x_[:, None, :]), LazyTensor(y_[None, :, :])
D_ij = ((x_i - y_j) ** 2).sum(dim=2)  # Symbolic (M,N,1) matrix of squared distances
K = (-D_ij / 2).exp()  # Symbolic (M,N,1) Gaussian kernel matrix

And create a random signal supported by the points \(y_j\):

b = np.random.randn(N, 1).astype(dtype)

Compare the performances of our block-sparse code with those of a dense implementation, on both CPU and GPU backends:

Note

The standard KeOps routine are already very efficient: on the GPU, speed-ups with multiscale, block-sparse schemes only start to kick on around the “20,000 points” mark as the skipped computations make up for the clustering and branching overheads.

backends = (
    (["CPU", "GPU"] if M * N < 4e8 else ["GPU"])
    if pykeops.config.gpu_available
    else ["CPU"]
)
for backend in backends:
    K.backend = backend  # Switch to CPU or GPU mode

    # GPU warm-up:
    a = K @ b

    start = time.time()
    K.ranges = None  # default
    a_full = K @ b
    end = time.time()
    t_full = end - start
    print(" Full  convolution, {} backend: {:2.4f}s".format(backend, end - start))

    start = time.time()
    K.ranges = ranges_ij  # block-sparsity pattern
    a_sparse = K @ b
    end = time.time()
    t_sparse = end - start
    print("Sparse convolution, {} backend: {:2.4f}s".format(backend, end - start))
    print(
        "Relative time : {:3d}% ({:3d}% including clustering), ".format(
            int(100 * t_sparse / t_full), int(100 * (t_sparse + t_cluster) / t_full)
        )
    )
    print(
        "Relative error:   {:3.4f}%".format(
            100 * np.sum(np.abs(a_sparse - a_full)) / np.sum(np.abs(a_full))
        )
    )
    print("")

 Full  convolution, CPU backend: 0.0378s
Sparse convolution, CPU backend: 0.0474s
Relative time : 125% (132% including clustering),
Relative error:   0.2364%

 Full  convolution, GPU backend: 0.0005s
Sparse convolution, GPU backend: 0.0005s
Relative time :  95% (656% including clustering),
Relative error:   0.2364%

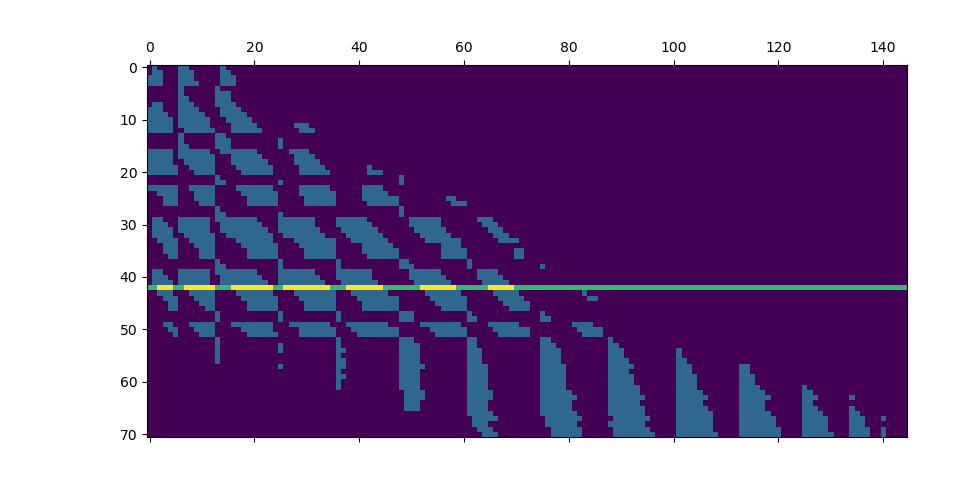
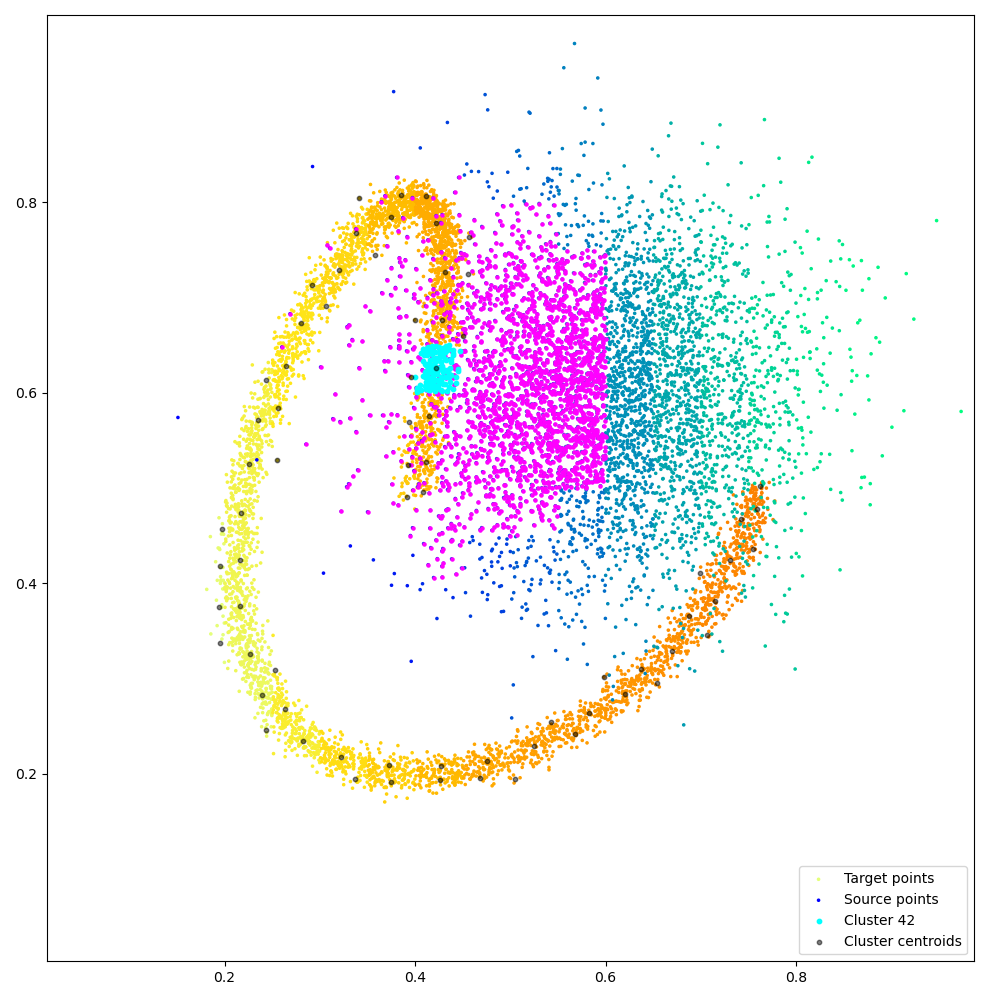
Fancy visualization: we display our coarse binary mask and highlight one of its lines, that corresponds to the cyan cluster and its magenta neighbors:

# Find the cluster centroid which is closest to the (.43,.6) point:
dist_target = np.sum(((x_centroids - np.array([0.43, 0.6]).astype(dtype)) ** 2), axis=1)
clust_i = np.argmin(dist_target)

if M + N <= 500000:
    ranges_i, slices_j, redranges_j = ranges_ij[0:3]
    start_i, end_i = ranges_i[clust_i]  # Indices of the points that make up our cluster
    start, end = (
        slices_j[clust_i - 1],
        slices_j[clust_i],
    )  # Ranges of the cluster's neighbors

    keep = keep.astype(float)
    keep[clust_i] += 2

    plt.ion()
    plt.matshow(keep)

    plt.figure(figsize=(10, 10))

    plt.scatter(
        x[:, 0],
        x[:, 1],
        c=x_labels,
        cmap=plt.cm.Wistia,
        s=25 * 500 / len(x),
        label="Target points",
    )
    plt.scatter(
        y[:, 0],
        y[:, 1],
        c=y_labels,
        cmap=plt.cm.winter,
        s=25 * 500 / len(y),
        label="Source points",
    )

    # Target clusters:
    for start_j, end_j in redranges_j[start:end]:
        plt.scatter(
            y[start_j:end_j, 0], y[start_j:end_j, 1], c="magenta", s=50 * 500 / len(y)
        )

    # Source cluster:
    plt.scatter(
        x[start_i:end_i, 0],
        x[start_i:end_i, 1],
        c="cyan",
        s=10,
        label="Cluster {}".format(clust_i),
    )

    plt.scatter(
        x_centroids[:, 0],
        x_centroids[:, 1],
        c="black",
        s=10,
        alpha=0.5,
        label="Cluster centroids",
    )

    plt.legend(loc="lower right")

    # sphinx_gallery_thumbnail_number = 2
    plt.axis("equal")
    plt.axis([0, 1, 0, 1])
    plt.tight_layout()
    plt.show(block=True)

• 
•