KernelSolve reduction (with LazyTensors)

Let’s see how to solve discrete deconvolution problems using the conjugate gradient solver provided by the pykeops.numpy.LazyTensor.solve() method of KeOps pykeops.numpy.LazyTensor.

Setup

Standard imports:

import time

import matplotlib.pyplot as plt
import numpy as np

from pykeops.numpy import Vi, Vj, Pm
import pykeops.config

Define our dataset:

N = 5000 if pykeops.config.gpu_available else 500  # Number of points
D = 2  # Dimension of the ambient space
Dv = 2  # Dimension of the vectors (= number of linear problems to solve)
sigma = 0.1  # Radius of our RBF kernel

x = np.random.rand(N, D)
b = np.random.rand(N, Dv)
g = np.array([0.5 / sigma**2])  # Parameter of the Gaussian RBF kernel

alpha = 0.01

KeOps internal conjugate gradient solver

print("Solving a Gaussian linear system, with {} points in dimension {}.".format(N, D))
start = time.time()
Kxx = (-Pm(g) * Vi(x).sqdist(Vj(x))).exp()
c = Kxx.solve(Vi(b), alpha=alpha)
end = time.time()
print("Timing (KeOps implementation):", round(end - start, 5), "s")

Solving a Gaussian linear system, with 5000 points in dimension 2.
Timing (KeOps implementation): 0.63238 s

Note

The pykeops.numpy.LazyTensor.solve() method uses a conjugate gradient solver and assumes that Kxx defines a symmetric, positive and definite linear reduction with respect to the alias "b" specified trough the third argument.

Apply our solver on arbitrary point clouds:

Scipy conjugate gradient

from scipy.sparse import diags
from scipy.sparse.linalg import aslinearoperator, cg
from scipy.sparse.linalg.interface import IdentityOperator

print("Solving a Gaussian linear system, with {} points in dimension {}.".format(N, D))
start = time.time()
A = aslinearoperator(diags(alpha * np.ones(N))) + aslinearoperator(Kxx)
c_sp = np.zeros((N, Dv))
for i in range(Dv):
    c_sp[:, i] = cg(A, b[:, i])[0]

end = time.time()
print("Timing (KeOps + scipy implementation):", round(end - start, 5), "s")

/home/code/keops/pykeops/pykeops/examples/numpy/plot_test_invkernel_numpy_helper.py:70: DeprecationWarning:

`scipy.sparse.linalg.interface.IdentityOperator` is deprecated along with the `scipy.sparse.linalg.interface` namespace. `scipy.sparse.linalg.interface.IdentityOperator` will be removed in SciPy 1.14.0, and the `scipy.sparse.linalg.interface` namespace will be removed in SciPy 2.0.0.

Solving a Gaussian linear system, with 5000 points in dimension 2.
Timing (KeOps + scipy implementation): 1.06901 s

Compare with a straightforward Numpy implementation:

start = time.time()
K_xx = alpha * np.eye(N) + np.exp(
    -g * np.sum((x[:, None, :] - x[None, :, :]) ** 2, axis=2)
)
c_np = np.linalg.solve(K_xx, b)
end = time.time()
print("Timing (Numpy implementation):", round(end - start, 5), "s")
print("Relative error (KeOps) = ", np.linalg.norm(c - c_np) / np.linalg.norm(c))
print("Relative error (KeOps + scipy)= ", np.linalg.norm(c - c_sp) / np.linalg.norm(c))

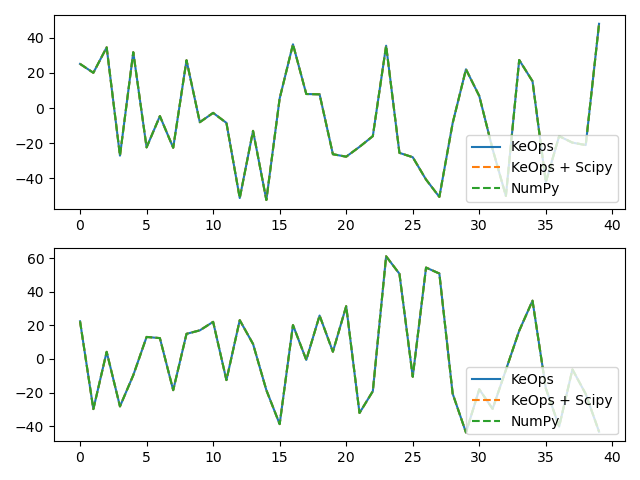
# Plot the results next to each other:
for i in range(Dv):
    plt.subplot(Dv, 1, i + 1)
    plt.plot(c[:40, i], "-", label="KeOps")
    plt.plot(c_sp[:40, i], "--", label="KeOps + Scipy")
    plt.plot(c_np[:40, i], "--", label="NumPy")
    plt.legend(loc="lower right")
plt.tight_layout()
plt.show()

Timing (Numpy implementation): 1.22777 s
Relative error (KeOps) =  4.903560602317892e-07
Relative error (KeOps + scipy)=  2.9595186339279965e-06