Note
Go to the end to download the full example code
K-means clustering - PyTorch API
The pykeops.torch.LazyTensor.argmin() reduction supported by KeOps pykeops.torch.LazyTensor allows us
to perform bruteforce nearest neighbor search with four lines of code.
It can thus be used to implement a large-scale
K-means clustering,
without memory overflows.
Note
For large and high dimensional datasets, this script outperforms its NumPy counterpart as it avoids transfers between CPU (host) and GPU (device) memories.
Setup
Standard imports:
import time
import torch
from matplotlib import pyplot as plt
from pykeops.torch import LazyTensor
use_cuda = torch.cuda.is_available()
dtype = torch.float32 if use_cuda else torch.float64
device_id = "cuda:0" if use_cuda else "cpu"
Simple implementation of the K-means algorithm:
def KMeans(x, K=10, Niter=10, verbose=True):
"""Implements Lloyd's algorithm for the Euclidean metric."""
start = time.time()
N, D = x.shape # Number of samples, dimension of the ambient space
c = x[:K, :].clone() # Simplistic initialization for the centroids
x_i = LazyTensor(x.view(N, 1, D)) # (N, 1, D) samples
c_j = LazyTensor(c.view(1, K, D)) # (1, K, D) centroids
# K-means loop:
# - x is the (N, D) point cloud,
# - cl is the (N,) vector of class labels
# - c is the (K, D) cloud of cluster centroids
for i in range(Niter):
# E step: assign points to the closest cluster -------------------------
D_ij = ((x_i - c_j) ** 2).sum(-1) # (N, K) symbolic squared distances
cl = D_ij.argmin(dim=1).long().view(-1) # Points -> Nearest cluster
# M step: update the centroids to the normalized cluster average: ------
# Compute the sum of points per cluster:
c.zero_()
c.scatter_add_(0, cl[:, None].repeat(1, D), x)
# Divide by the number of points per cluster:
Ncl = torch.bincount(cl, minlength=K).type_as(c).view(K, 1)
c /= Ncl # in-place division to compute the average
if verbose: # Fancy display -----------------------------------------------
if use_cuda:
torch.cuda.synchronize()
end = time.time()
print(
f"K-means for the Euclidean metric with {N:,} points in dimension {D:,}, K = {K:,}:"
)
print(
"Timing for {} iterations: {:.5f}s = {} x {:.5f}s\n".format(
Niter, end - start, Niter, (end - start) / Niter
)
)
return cl, c
K-means in 2D
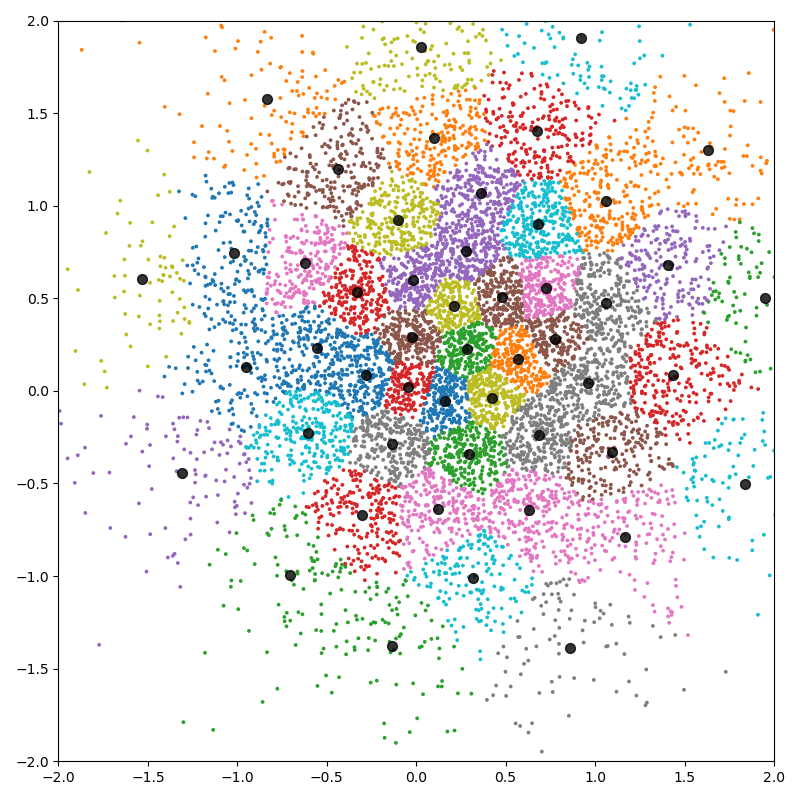
First experiment with N=10,000 points in dimension D=2, with K=50 classes:
N, D, K = 10000, 2, 50
Define our dataset:
x = 0.7 * torch.randn(N, D, dtype=dtype, device=device_id) + 0.3
Perform the computation:
cl, c = KMeans(x, K)
K-means for the Euclidean metric with 10,000 points in dimension 2, K = 50:
Timing for 10 iterations: 0.01042s = 10 x 0.00104s
Fancy display:
plt.figure(figsize=(8, 8))
plt.scatter(x[:, 0].cpu(), x[:, 1].cpu(), c=cl.cpu(), s=30000 / len(x), cmap="tab10")
plt.scatter(c[:, 0].cpu(), c[:, 1].cpu(), c="black", s=50, alpha=0.8)
plt.axis([-2, 2, -2, 2])
plt.tight_layout()
plt.show()
KeOps is a versatile library: we can add support for the cosine similarity with a few lines of code.
def KMeans_cosine(x, K=10, Niter=10, verbose=True):
"""Implements Lloyd's algorithm for the Cosine similarity metric."""
start = time.time()
N, D = x.shape # Number of samples, dimension of the ambient space
c = x[:K, :].clone() # Simplistic initialization for the centroids
# Normalize the centroids for the cosine similarity:
c = torch.nn.functional.normalize(c, dim=1, p=2)
x_i = LazyTensor(x.view(N, 1, D)) # (N, 1, D) samples
c_j = LazyTensor(c.view(1, K, D)) # (1, K, D) centroids
# K-means loop:
# - x is the (N, D) point cloud,
# - cl is the (N,) vector of class labels
# - c is the (K, D) cloud of cluster centroids
for i in range(Niter):
# E step: assign points to the closest cluster -------------------------
S_ij = x_i | c_j # (N, K) symbolic Gram matrix of dot products
cl = S_ij.argmax(dim=1).long().view(-1) # Points -> Nearest cluster
# M step: update the centroids to the normalized cluster average: ------
# Compute the sum of points per cluster:
c.zero_()
c.scatter_add_(0, cl[:, None].repeat(1, D), x)
# Normalize the centroids, in place:
c[:] = torch.nn.functional.normalize(c, dim=1, p=2)
if verbose: # Fancy display -----------------------------------------------
if use_cuda:
torch.cuda.synchronize()
end = time.time()
print(
f"K-means for the cosine similarity with {N:,} points in dimension {D:,}, K = {K:,}:"
)
print(
"Timing for {} iterations: {:.5f}s = {} x {:.5f}s\n".format(
Niter, end - start, Niter, (end - start) / Niter
)
)
return cl, c
Timings are similar to the Euclidean case:
cl, c = KMeans_cosine(x, K)
K-means for the cosine similarity with 10,000 points in dimension 2, K = 50:
Timing for 10 iterations: 0.02773s = 10 x 0.00277s
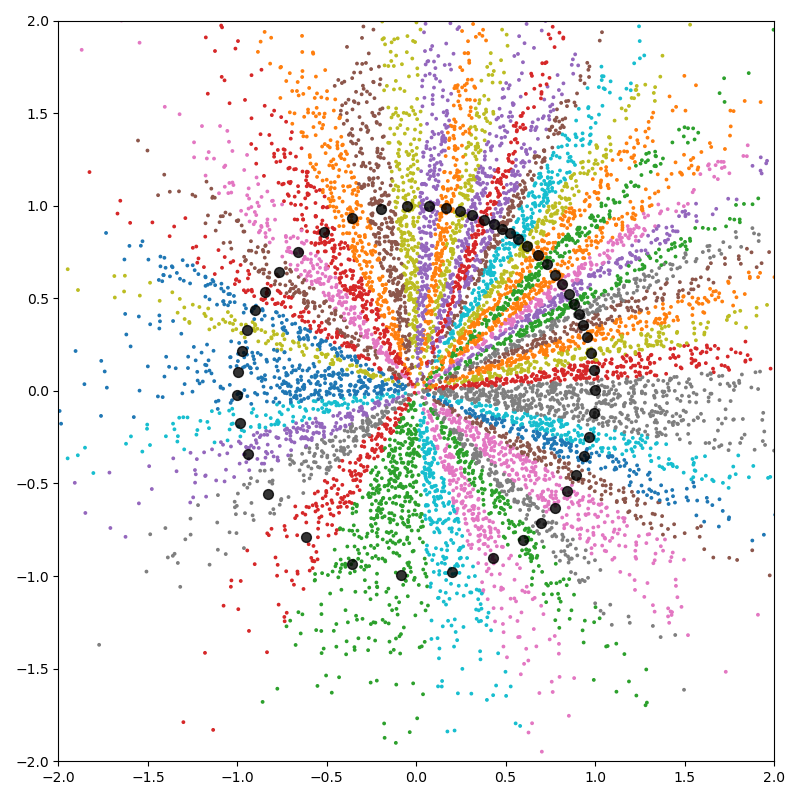
Clusters behave as slices around the origin:
plt.figure(figsize=(8, 8))
plt.scatter(x[:, 0].cpu(), x[:, 1].cpu(), c=cl.cpu(), s=30000 / len(x), cmap="tab10")
plt.scatter(c[:, 0].cpu(), c[:, 1].cpu(), c="black", s=50, alpha=0.8)
plt.axis([-2, 2, -2, 2])
plt.tight_layout()
plt.show()
K-means in dimension 100
Second experiment with N=1,000,000 points in dimension D=100, with K=1,000 classes:
if use_cuda:
N, D, K = 1000000, 100, 1000
x = torch.randn(N, D, dtype=dtype, device=device_id)
cl, c = KMeans(x, K)
cl, c = KMeans_cosine(x, K)
K-means for the Euclidean metric with 1,000,000 points in dimension 100, K = 1,000:
Timing for 10 iterations: 0.49893s = 10 x 0.04989s
K-means for the cosine similarity with 1,000,000 points in dimension 100, K = 1,000:
Timing for 10 iterations: 0.41319s = 10 x 0.04132s
Total running time of the script: (0 minutes 1.434 seconds)