K-means clustering - NumPy API

The pykeops.numpy.LazyTensor.argmin() reduction supported by KeOps pykeops.numpy.LazyTensor allows us to perform bruteforce nearest neighbor search with four lines of code. It can thus be used to implement a large-scale K-means clustering, without memory overflows.

Note

For large and high dimensional datasets, this script is outperformed by its PyTorch counterpart which avoids transfers between CPU (host) and GPU (device) memories.

Setup

Standard imports:

import time

import numpy as np
from matplotlib import pyplot as plt

from pykeops.numpy import LazyTensor
import pykeops.config

dtype = "float32"  # May be 'float32' or 'float64'

Simple implementation of the K-means algorithm:

def KMeans(x, K=10, Niter=10, verbose=True):
    N, D = x.shape  # Number of samples, dimension of the ambient space

    # K-means loop:
    # - x  is the point cloud,
    # - cl is the vector of class labels
    # - c  is the cloud of cluster centroids
    start = time.time()
    c = np.copy(x[:K, :])  # Simplistic random initialization
    x_i = LazyTensor(x[:, None, :])  # (Npoints, 1, D)

    for i in range(Niter):
        c_j = LazyTensor(c[None, :, :])  # (1, Nclusters, D)
        D_ij = ((x_i - c_j) ** 2).sum(
            -1
        )  # (Npoints, Nclusters) symbolic matrix of squared distances
        cl = D_ij.argmin(axis=1).astype(int).reshape(N)  # Points -> Nearest cluster

        Ncl = np.bincount(cl).astype(dtype)  # Class weights
        for d in range(D):  # Compute the cluster centroids with np.bincount:
            c[:, d] = np.bincount(cl, weights=x[:, d]) / Ncl

    end = time.time()

    if verbose:
        print(
            "K-means example with {:,} points in dimension {:,}, K = {:,}:".format(
                N, D, K
            )
        )
        print(
            "Timing for {} iterations: {:.5f}s = {} x {:.5f}s\n".format(
                Niter, end - start, Niter, (end - start) / Niter
            )
        )

    return cl, c

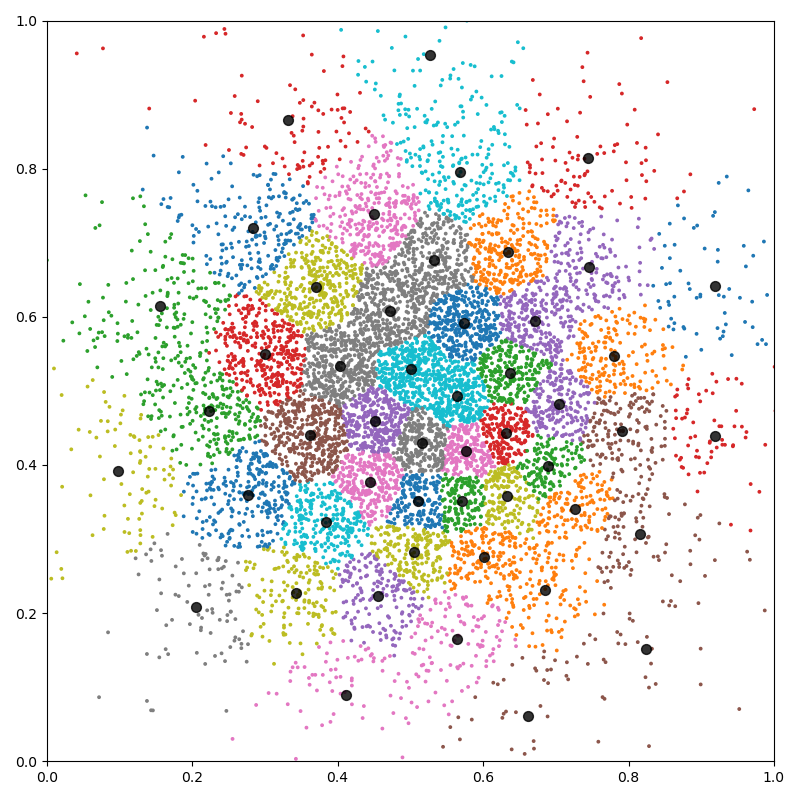
K-means in 2D

First experiment with N=10,000 points in dimension D=2, with K=50 classes:

N, D, K = 10000, 2, 50

Define our dataset:

x = np.random.randn(N, D).astype(dtype) / 6 + 0.5

Perform the computation:

cl, c = KMeans(x, K)

K-means example with 10,000 points in dimension 2, K = 50:
Timing for 10 iterations: 0.00458s = 10 x 0.00046s

Fancy display:

plt.figure(figsize=(8, 8))
plt.scatter(x[:, 0], x[:, 1], c=cl, s=30000 / len(x), cmap="tab10")
plt.scatter(c[:, 0], c[:, 1], c="black", s=50, alpha=0.8)
plt.axis([0, 1, 0, 1])
plt.tight_layout()
plt.show()

K-means in dimension 100

Second experiment with N=1,000,000 points in dimension D=100, with K=1,000 classes:

if pykeops.config.gpu_available:
    N, D, K = 1000000, 100, 1000
    x = np.random.randn(N, D).astype(dtype)
    cl, c = KMeans(x, K)

K-means example with 1,000,000 points in dimension 100, K = 1,000:
Timing for 10 iterations: 5.68102s = 10 x 0.56810s